결정 트리(Decision Tree)

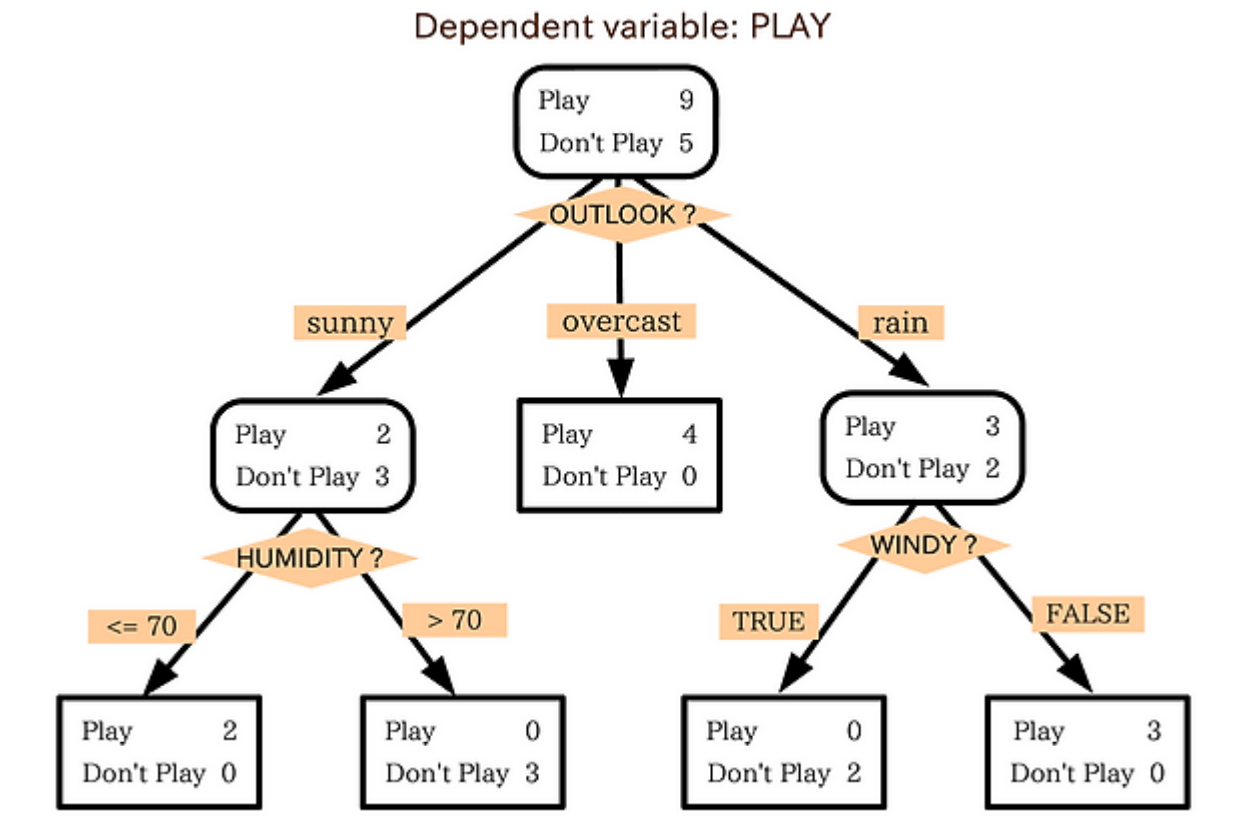
결정 트리 분류기는 설명이 중요할 때 아주 유용한 모델이다.

일련의 질문에 대한 결정을 통해 데이터를 분해하는 모델로 생각할 수 있다.

훈련 데이터에 있는 특성을 기반으로 샘플의 클래스 레이블을 추정할 수 있는 일련의 질문을 학습

결정 알고리즘을 사용하면 트리의 루트(root)에서 시작해서 정보 이득(information gain, IG)가 최대가 되는

특성으로 데이터를 나눈다.

반복과정을 통해 리프노드가 순수해질 때까지 모든 자식 노드에서 이 분할 작업을 반복한다.

이때, 각 노드의 모든 훈련 샘플은 동일한 클래스에 속한다.

실제로 위와 같이 반복할 시 과대적합될 가능성이 크다.

따라서 트리의 최대 깊이를 제한하여 트리를 가지치기(pruning)한다.

정보 이득 최대화: 자원을 최대로 활용

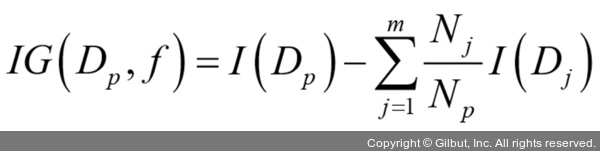
정보 이득은 위와 같다.

결정 트리는 위의 목적함수가 최대화한다

위의 식을 쉽게 말하면 정보이득은 단순히 부모 노드의 불순도와 자식 노드의 불순도 합의 차이다.

이진 결정 트리에서 널리 사용되는 4개의 불순도 지표 또는 분할 조건은

1) 지니 불순도(GIni impurity, I(G) )

2) 엔트로피(Entropy. I(H))

3) 분류 오차(Classification error, I(E) )

엔트로피

클래스 분포가 균일하면, 엔트로피는 최대가 된다.

이진 클래스의 경우 p가 0이거나 1이되면 엔트로피는 0이다.

p가 0.5가 되면 엔트로피는 1이 된다.

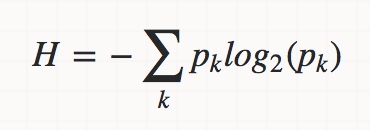
지니 불순도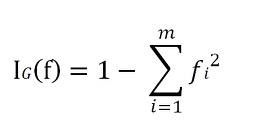

엔트로피와 유사하게 지니 불순도 또한 클래스가 완벽하게 섞였을 때, 최대가 된다.

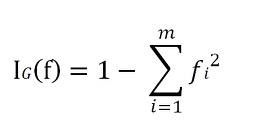
실제로 지니 불순도와 엔트로피의 계산값은 매우 유사함

불순도 조건을 바꾸어 트리를 평가하는 것보다는 가지치기 수준을 바꿔가며, 튜닝하는 것이 더 효과적임

분류 오차

I(E) = 1 - max(p( i | t )

가지치기는 좋은 기준이지만 노드의 클래스 확률 변화에 덜 민감하기 때문에 결정 트리를 구성하는데 권장되지는 않는다.

불순도 인덱스

import matplotlib.pyplot as plt

import numpy as np

def gini(p):

return (p)*(1-(p))+(1-p)*(1-(1-p))

def entropy(p):

return -p*np.log2(p)-(1-p)*np.log2((1-p))

def error(p):

return 1-np.max([p, 1-p])

x=np.arange(0.0, 1.0, 0.01)

ent=[entropy(p) if p!=0 else None for p in x]

sc_ent=[e*0.5 if e else None for e in ent]

err=[error(i) for i in x]

fig=plt.figure()

ax=plt.subplot(111)

for i, lab, ls ,c in zip([ent, sc_ent, gini(x), err], ['Entropy', 'Entropy (scaled)', 'Gini impurity', 'Misclassification error'], ['-', '-', '--', '-.'], ['black', 'lightgray', 'red', 'green', 'cyan']):

line=ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)

ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15), ncol=5, fancybox=True, shadow=False)

ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')

ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')

plt.ylim([0, 1.1])

plt.xlabel('p(i=1)')

plt.ylabel('impurity index')

plt.show()

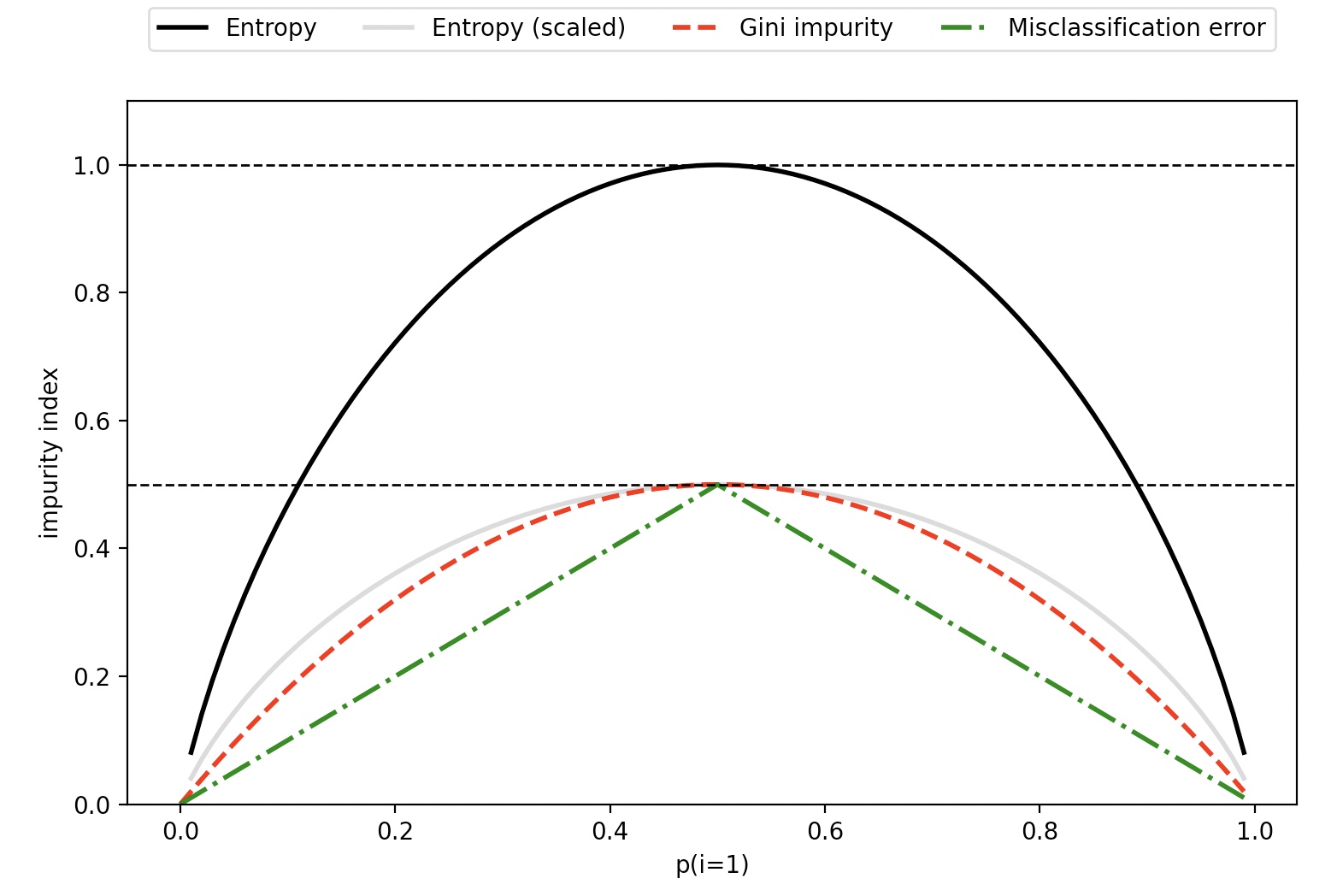
scaled entropy는 entropy와 분류 오차의 중간이 지니 불순도임을 관찰하기 위해 만든 조정된 엔트로피(entropy/2)

making Decision Tree

결정 트리는 특성 공간을 사각 공간으로 나눈다. 따라서 복잡한 경계를 만들 수 있다.

( 결정 트리가 깊어질 수록 결정 경계가 복잡해지고, 과대적합되기 쉽다. )

scikit learn을 이용한 지니 불순도 조건의 최대 깊이 4인 결정 트리

DecisionTreeClassifier 의 criterion 매개변수의 기본값은 지니 불순도를 의미하는 ‘gini’ 이다.

max_depth의 기본값은 None으로 모든 리프 노드가 순수해질 때까지 트리가 성장한다.

노드 분할을 위해 고려할 특성의 개수를 지정하는 max_features의 기본값은 None으로 전체 특성을 사용

from sklearn.tree import DecisionTreeClassifier

tree=DecisionTreeClassifier(criterion='gini', max_depth=4, random_state=1)

tree.fit(X_train, y_train)

X_combined=np.vstack((X_train, X_test))

y_combined=np.hstack((y_train, y_test))

plot_decision_regions(X_combined, y_combined, classifier=tree, test_idx=range(105, 150))

plt.xlabel('petal length [cm]')

plt.ylabel('petal width [cm]')

plt.legend(loc='upper left')

plt.tight_layout()

plt.show()

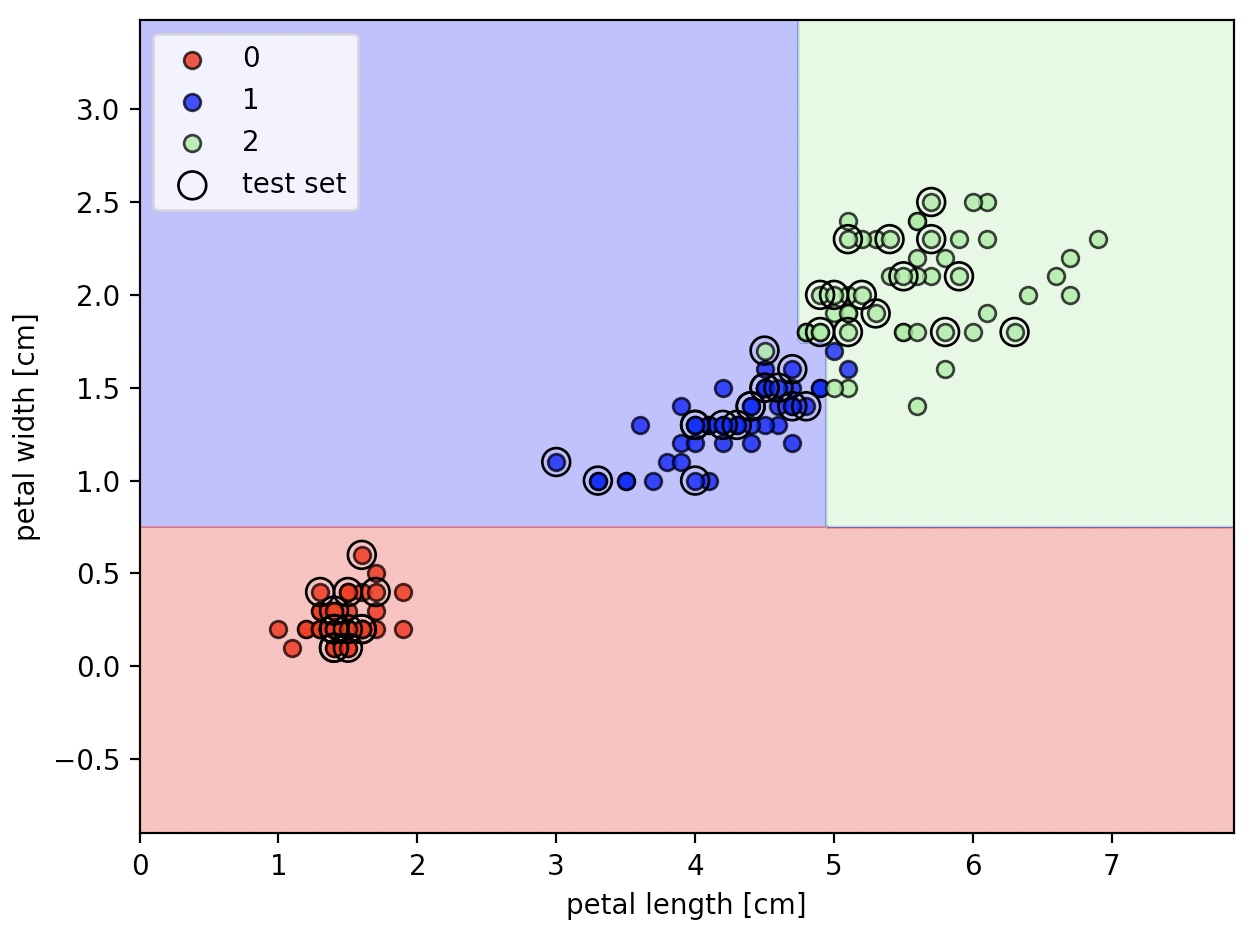
scikit learn의 기본 plot_tree를 이용한 결정 트리 이미지

tree_model=tree.fit(X_train, y_train)

from sklearn import tree

tree_model=tree.fit(X_train, y_train)

tree.plot_tree(tree_model)

plt.show()

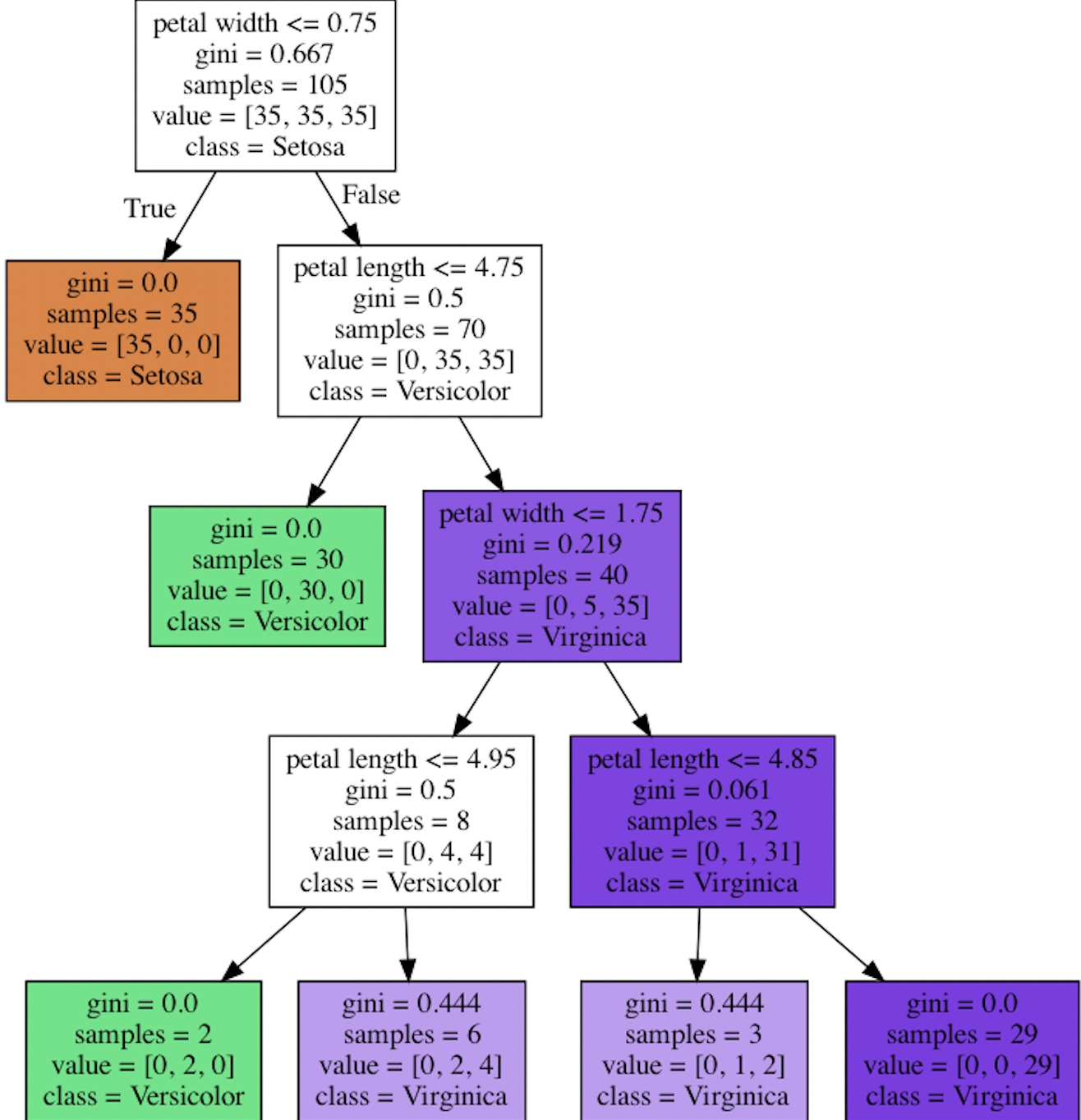
GraphVIz를 이용한 결정 트리 이미지

사이킷런도 .dot 파일로 추출할 수 있는 기능을 가지고 있지만, GraphViz를 이용하면,

이 파일을 시각화 할 수 있다.

추가적으로 PyDotPlus를 사용

pip3 install graphviz

pip3 install pydotplus

from pydotplus import graph_from_dot_data

from sklearn.tree import export_graphviz

dot_data=export_graphviz(tree, filled=True, class_names=['Setosa', 'Versicolor', 'Virginica'], feature_names=['petal length', 'petal width'], out_file=None)

graph=graph_from_dot_data(dot_data)

graph.write_png('tree.png')

from sklearn.tree import DecisionTreeClassifier

tree=DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=1)

tree.fit(X_train, y_train)

X_combined=np.vstack((X_train, X_test))

y_combined=np.hstack((y_train, y_test))

from pydotplus import graph_from_dot_data

from sklearn.tree import export_graphviz

dot_data=export_graphviz(tree, filled=True, class_names=['Setosa', 'Versicolor', 'Virginica'], feature_names=['petal length', 'petal width'], out_file=None)

graph=graph_from_dot_data(dot_data)

graph.write_png('tree.png')

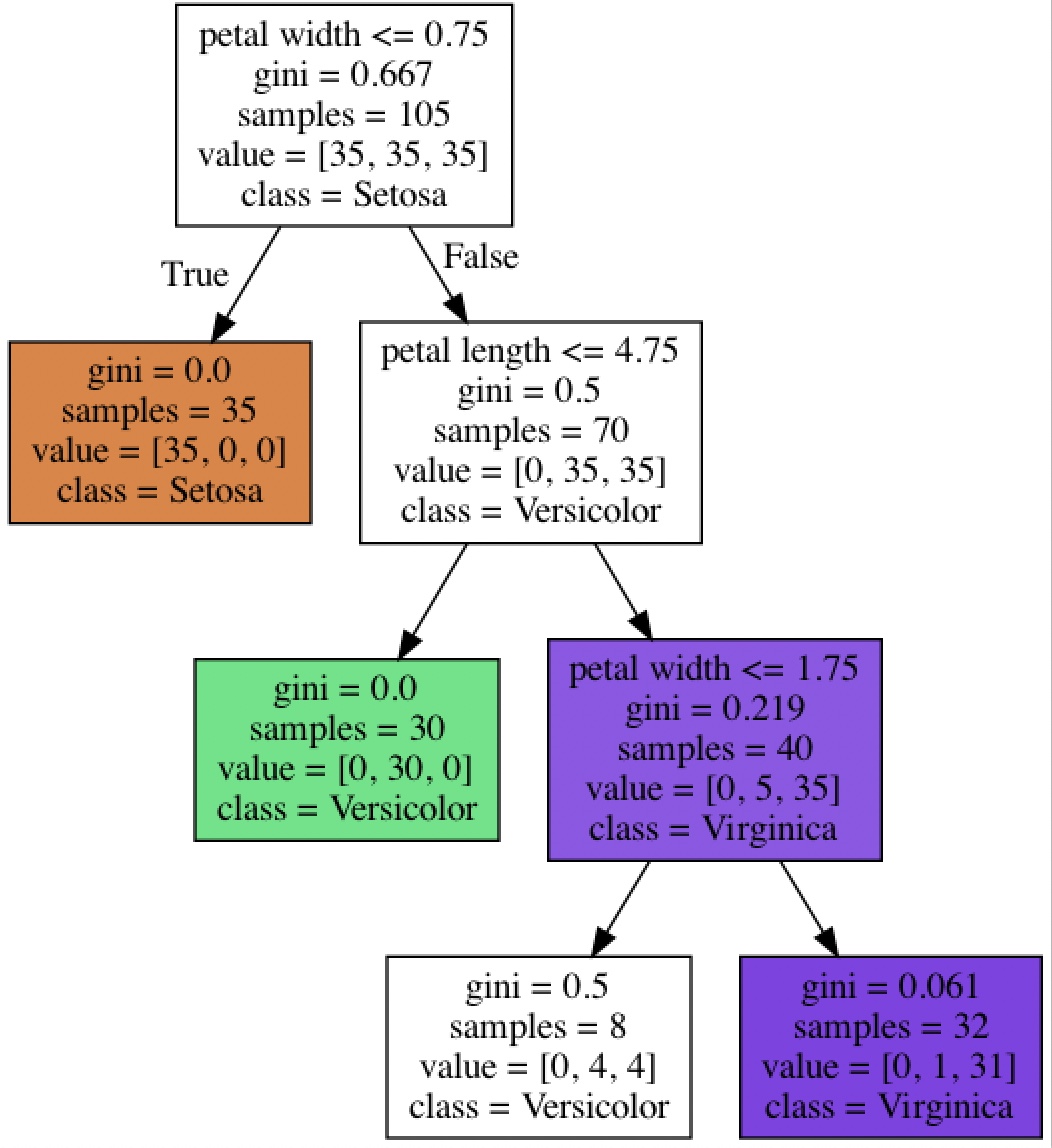
max_depth를 4에서 3으로 바꾸었을 때(prunning)

max_depth 외에 사이킷런의 결정 트리에서 지원하는 대표적인 사전 가지치기 설정

max_leaf_nodes: 리프 노드의 최대 개수를 지정.

min_samples_leaf: 리프 노드가 되기 위한 최소 샘플 개수나 샘플의 비율을 지정. 기본값: 1

min_saples_split: 노드 분할을 위한 최소 샘플 개수나 샘플의 비율을 지정. 기본값: 2

min_impurity_decrease: 노드 분할이 감소시킬 최소 불순도를 지정. 기본값: 0

min_impurity_split: 트리 성장을 멈출 불순도 임계 값. 기본값: (이 후 사이킷런 0.25에서 삭제)

사이킷런 0.22 버전 이후 사후 가지치기 중 하나인 비용 복잡도 가지치기(cost complexity pruning) 기능이 추가됨

현재 노드의 복잡도와 하위 트리의 복잡도 차이가 가장 작은 가지를 제거

ccp_alpha 매개변수값이 클수록 가지치기 정도가 늘어난다. 기본값 0(가지치기 수행 X)